Kermack-Mckendrick阈模型在传染病流行病学中的应用
作者：林太斌
单位：林太斌 福建医科大学流行病学教研室(福州 350004)
关键词：Kermack-Mckendrick阈模型；流行过程；传染性接触率
福建医科大学学报990114 目的 探讨Kermack-Mckendrick(K-M)模型在传染病流行学的应用性。 方法 以上海某托儿所一起水痘流行过程的资料，应用K-M模型进行模拟。 结果 经拟合，实际资料同模型拟合良好。 结论 K-M模型适于描述某种急性传染病被引入某封闭人群后所发生的流行过程。
Application of Kermack-Mckendrick Threshold Model in Infectious Disease Epidemiology
Lin Taibin
, http://www.100md.com
(Department of Epidemiology, Fujian Medical University, Fuzhou, 350004)
Objective To study application of Kermack-Mckendrick threshold model in infectious disease epidemiology. Methods To apply Kermack-Mckendrick to stimulate a chicken pox epidemic in Shanghai certain child-care centre. Results Total infected cases calculated by the formula is equal to the practical data. Conclusion Kermack-Mckendrick threshold model is suited to descriptive the epidemic process of certain acute infectious disease that is propagated to the separated population.
, 百拇医药
Key words Kermack-Mckendrick threshold model; epidemic process; contagious rate
本世纪40年代，Kermack-Mckendrick研究传染病在家庭及住户内传播的规律，提出了著名的阈定理(threshold theorem)。嗣后，他们又依据该定理及若干项假设[1]，建立了Kermack-Mckendrick阈模型(K-M模型)。鉴于未见到国内文献用此模型研究疾病流行过程的报道，本文拟对流行病著述一再引用的上海某托儿所一起水痘流行过程资料，应用K-M模型进行模拟，并对模拟结果进行讨论。
1 K-M模型的介绍
1.1 K-M模型的数学表达式
, 百拇医药
式中：S:易感人群;
I:传染病病例(感染者)人数;
R:免疫者人数;
β:传染性接触率;
γ:恢复率.
此模型适于模拟由S-I-R类型传染病在封闭人群中流行过程。
设初始条件为S(0)个易感者，I(0)个感染者，通过求解以上微分方程组，可得直观图象(附图)。
附图 S(0)，
与[S(0)-S(∞)]的关系
, 百拇医药
(1)当S(0)>时，疾病才会流行；当S(0)＝时，I(t)达到最大值。
(2)初始I(0)一般较小，若此时增大恢复率γ，同时降低接触率β，则可防止流行。
(3)当S(0)-<<时，被感染总人数 S(0)-S(∞)近似于2[S(0)-]。
, 百拇医药
1.2 参数估计
解微分方程，由(1)，(2)可推出(过程略)：
R= -Ln S+C (C为常数项) (5)
由(4)得 I = N-S+Ln S-C (6)
由R(0)，S(0)，并经适当选择，确定参数C来判断拟合。
由S(0)，与[S(0)-S(∞)]的近似关系，得：≈S(0)-
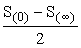(7)
, 百拇医药
2 模型的应用
例 1950年上海某托儿所发生一起水痘流行，该所儿童总人数n= 196人，I(0)= 1 , S(0)=155，S(0)-S(∞)=96 。全部流行期79天，流行过程病例成批(代)出现，每代相隔约15天。各代病例数、易感者数及相隔时间见表1。
表1 上海某托儿所水痘病例数、易感者数及相隔时间 代
病例数
易感者数
相隔时间(天)
1
1
, 百拇医药 155
15
2
2
153
15
3
14
139
17
4
38
101
14
, 百拇医药
5
34
67
6
7
33
合计
96
以初始值S(0)，S(0)-S(∞)代入公式(7)，得≈155-
=107
, http://www.100md.com 经尝试，取=101代入(5)，得C = 549.39来拟合最佳(表2)。表2 拟合过程公式I=N-S+Ln S-C 单位时间
(t)
易感者数
(S)
感染者数
(I)
计算式
t0
155
, http://www.100md.com
1
1(初例)
t1
154
1
196-155+101ln155-549.39＝0.99
t2
153
1
196-154+101ln154-549.39＝1.34
t3
, 百拇医药
151
2
196-153+101ln153-549.39＝1.68
t4
149
2
196-151+101ln151-549.39＝2.36
t5
146
3
196-149+101ln149-549.39＝3.00
, 百拇医药
t6
142
4
196-146+101ln146-549.39＝3.95
t7
137
5
196-142+101ln142-549.39＝5.15
t8
130
7
, 百拇医药 196-137+101ln137-549.39＝6.53
t9
122
8
196-130+101ln130-549.39＝8.23
t10
112
10
196-122+101ln122-549.39＝9.82
t11
101
, http://www.100md.com
11
196-112+101ln112-549.39＝11.18
t12
89
12
196-101+101ln101-549.39＝11.74
t13
78
11
196- 89 +101ln 89 -549.39＝10.96
t14
, 百拇医药
69
9
196- 78 +101ln 78 -549.39＝8.64
t15
64
5
196- 69 +101ln 69 -549.39＝5.25
t16
61
3
196- 64 +101ln 64 -549.39＝2.66
, 百拇医药
t17
60
1
196- 61+101ln 61 -549.39＝0.81
合计
—
96
—
3 讨 论
数学模型是理论流行病学研究的主要工具。苏德隆[2]率先把Soper模型加以修改，模拟了上海托儿所一次水痘流行过程，用于流行病学教学。但苏德隆模型结构中，传染率是以病例与传染性接触率乘积来表示，而实际上，人群中疾病动力学所反映的并非这两者呈简单相乘的关系，而是一种指数关系。故在后来流行病学教材中[3]作了修正，引入了Reed-Frost原模型中[1-qCt]和增加了[
]。前一项为传染率的表达式；后一项为苏德隆模型和李婉先模型的共有项，它在数理上解决了对1～5代水痘病例的模拟问题。
, 百拇医药
对[
]，苏德隆和李婉先的共同解释是,免疫者的增多，引起了免疫屏障的作用。曾光[4,5]对此持有异议，他认为在一个类似封闭的人群中，免疫者的产生不影响该群体的传染性接触率，因而不可能产生免疫屏障作用。同时，他还指出，Reed-Frost原模型拟合实际资料欠佳，主要是由于模型中未考虑隐性感染者的缘故。为此，他在其“修改型模型”[5]中引进了隐性感染者这一因素，取得了较好的拟合结果。从理论上讲，曾光模型更为接近实际过程。而事实上，该模型只适合在隐性感染比例甚高的传染病中应用。此外，由于该模型增加了参数，不仅在计算上增大难度，而且在统计上降低了可靠性。
K-M模型与Reed-Frost模型(包括修改型)，基本假设条件相同，并适用研究急性接触性传染病。惟后者尚需满足如下两个条件：一是潜伏期近乎恒定；二是病例成批(代)出现。故而病例统计及适合度检验均以“代”为框架。K-M模型不受以上条件限制，模型中单位时间t，是一个应变量，受制于模型拟合时给定的条件。本例整个流行期79天，以初始时间t0为起点，相邻单位时间相隔约5天(79/17)，而且自t0起，每隔3个单位时间(约15天)所对应的日期与表1中各代中位潜伏期基本吻合。虽然按单位时间计算的理论例数难于与按代统计的实际例数进行拟合，但经拟合，实际资料同模型拟合良好。
, 百拇医药
K-M模型涉及一组微分方程，看似复杂，实则计算起来并不难，尤其能用图示表达各要素之间的数量关系，更适于教学。此外，本模型引入项，β为传染性接触率，γ为恢复率，即感染者转变为下一代免疫者的概率，这是动力学模型两个敏感参数，使得模型具有更大的普适性。当然，数学模型优点只表现在数学方面是不够的，重要的是对方程中各项的设计和各种状态的转移作出合理的解释。应当说K-M模型结构中未考虑隐性感染者，这固然使模型显得较为简洁与明快，但反过来也使其应用范围受到限制。本文仅对国内记录较完整的一起传染病在特定人群中流行过程作模拟，K-M模型是否能成功应用于其他场合，尚待进一步考验。
参考文献
[1]沈福民. 理论流行病学. 见：耿贯一(主编). 流行病学. 第1卷.第2版. 北京：人民卫生出版社, 1995: 288～290
, http://www.100md.com
[2]苏德隆(主编). 流行病学. 北京: 人民卫生出版社, 1964: 90～94
[3]连志浩(主编). 流行病学. 北京: 人民卫生出版社, 1994: 127～128
[4]曾 光(主编).现代流行病学方法与应用. 北京:北京医科大学、中国协和医科大学联合出版社, 1994: 203～208
[5]曾 光. 一种Reed-Frost确定型模型的修改型及其应用. 中华流行病学杂志, 1986; 7: 366
(收稿：1998-11-05 修回：1999-01-28), http://www.100md.com
单位：林太斌 福建医科大学流行病学教研室(福州 350004)
关键词：Kermack-Mckendrick阈模型；流行过程；传染性接触率
福建医科大学学报990114 目的 探讨Kermack-Mckendrick(K-M)模型在传染病流行学的应用性。 方法 以上海某托儿所一起水痘流行过程的资料，应用K-M模型进行模拟。 结果 经拟合，实际资料同模型拟合良好。 结论 K-M模型适于描述某种急性传染病被引入某封闭人群后所发生的流行过程。
Application of Kermack-Mckendrick Threshold Model in Infectious Disease Epidemiology
Lin Taibin
, http://www.100md.com
(Department of Epidemiology, Fujian Medical University, Fuzhou, 350004)
Objective To study application of Kermack-Mckendrick threshold model in infectious disease epidemiology. Methods To apply Kermack-Mckendrick to stimulate a chicken pox epidemic in Shanghai certain child-care centre. Results Total infected cases calculated by the formula is equal to the practical data. Conclusion Kermack-Mckendrick threshold model is suited to descriptive the epidemic process of certain acute infectious disease that is propagated to the separated population.
, 百拇医药
Key words Kermack-Mckendrick threshold model; epidemic process; contagious rate
本世纪40年代，Kermack-Mckendrick研究传染病在家庭及住户内传播的规律，提出了著名的阈定理(threshold theorem)。嗣后，他们又依据该定理及若干项假设[1]，建立了Kermack-Mckendrick阈模型(K-M模型)。鉴于未见到国内文献用此模型研究疾病流行过程的报道，本文拟对流行病著述一再引用的上海某托儿所一起水痘流行过程资料，应用K-M模型进行模拟，并对模拟结果进行讨论。
1 K-M模型的介绍
1.1 K-M模型的数学表达式
, 百拇医药
式中：S:易感人群;
I:传染病病例(感染者)人数;
R:免疫者人数;
β:传染性接触率;
γ:恢复率.
此模型适于模拟由S-I-R类型传染病在封闭人群中流行过程。
设初始条件为S(0)个易感者，I(0)个感染者，通过求解以上微分方程组，可得直观图象(附图)。
附图 S(0)，
与[S(0)-S(∞)]的关系, 百拇医药
(1)当S(0)>
时，疾病才会流行；当S(0)＝时，I(t)达到最大值。(2)初始I(0)一般较小，若此时增大恢复率γ，同时降低接触率β，则可防止流行。
(3)当S(0)-
<<时，被感染总人数 S(0)-S(∞)近似于2[S(0)-]。, 百拇医药
1.2 参数估计
解微分方程，由(1)，(2)可推出(过程略)：
R= -
Ln S+C (C为常数项) (5)由(4)得 I = N-S+
Ln S-C (6)由R(0)，S(0)，并经适当选择
，确定参数C来判断拟合。由S(0)，
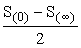与[S(0)-S(∞)]的近似关系，得：≈S(0)- (7), 百拇医药
2 模型的应用
例 1950年上海某托儿所发生一起水痘流行，该所儿童总人数n= 196人，I(0)= 1 , S(0)=155，S(0)-S(∞)=96 。全部流行期79天，流行过程病例成批(代)出现，每代相隔约15天。各代病例数、易感者数及相隔时间见表1。
表1 上海某托儿所水痘病例数、易感者数及相隔时间 代
病例数
易感者数
相隔时间(天)
1
1
, 百拇医药 155
15
2
2
153
15
3
14
139
17
4
38
101
14
, 百拇医药
5
34
67
6
7
33
合计
96
以初始值S(0)，S(0)-S(∞)代入公式(7)，得
≈155-=107, http://www.100md.com 经尝试，取
=101代入(5)，得C = 549.39来拟合最佳(表2)。表2 拟合过程公式I=N-S+Ln S-C 单位时间(t)
易感者数
(S)
感染者数
(I)
计算式
t0
155
, http://www.100md.com
1
1(初例)
t1
154
1
196-155+101ln155-549.39＝0.99
t2
153
1
196-154+101ln154-549.39＝1.34
t3
, 百拇医药
151
2
196-153+101ln153-549.39＝1.68
t4
149
2
196-151+101ln151-549.39＝2.36
t5
146
3
196-149+101ln149-549.39＝3.00
, 百拇医药
t6
142
4
196-146+101ln146-549.39＝3.95
t7
137
5
196-142+101ln142-549.39＝5.15
t8
130
7
, 百拇医药 196-137+101ln137-549.39＝6.53
t9
122
8
196-130+101ln130-549.39＝8.23
t10
112
10
196-122+101ln122-549.39＝9.82
t11
101
, http://www.100md.com
11
196-112+101ln112-549.39＝11.18
t12
89
12
196-101+101ln101-549.39＝11.74
t13
78
11
196- 89 +101ln 89 -549.39＝10.96
t14
, 百拇医药
69
9
196- 78 +101ln 78 -549.39＝8.64
t15
64
5
196- 69 +101ln 69 -549.39＝5.25
t16
61
3
196- 64 +101ln 64 -549.39＝2.66
, 百拇医药
t17
60
1
196- 61+101ln 61 -549.39＝0.81
合计
—
96
—
3 讨 论
数学模型是理论流行病学研究的主要工具。苏德隆[2]率先把Soper模型加以修改，模拟了上海托儿所一次水痘流行过程，用于流行病学教学。但苏德隆模型结构中，传染率是以病例与传染性接触率乘积来表示，而实际上，人群中疾病动力学所反映的并非这两者呈简单相乘的关系，而是一种指数关系。故在后来流行病学教材中[3]作了修正，引入了Reed-Frost原模型中[1-qCt]和增加了[
]。前一项为传染率的表达式；后一项为苏德隆模型和李婉先模型的共有项，它在数理上解决了对1～5代水痘病例的模拟问题。, 百拇医药
对[
]，苏德隆和李婉先的共同解释是,免疫者的增多，引起了免疫屏障的作用。曾光[4,5]对此持有异议，他认为在一个类似封闭的人群中，免疫者的产生不影响该群体的传染性接触率，因而不可能产生免疫屏障作用。同时，他还指出，Reed-Frost原模型拟合实际资料欠佳，主要是由于模型中未考虑隐性感染者的缘故。为此，他在其“修改型模型”[5]中引进了隐性感染者这一因素，取得了较好的拟合结果。从理论上讲，曾光模型更为接近实际过程。而事实上，该模型只适合在隐性感染比例甚高的传染病中应用。此外，由于该模型增加了参数，不仅在计算上增大难度，而且在统计上降低了可靠性。K-M模型与Reed-Frost模型(包括修改型)，基本假设条件相同，并适用研究急性接触性传染病。惟后者尚需满足如下两个条件：一是潜伏期近乎恒定；二是病例成批(代)出现。故而病例统计及适合度检验均以“代”为框架。K-M模型不受以上条件限制，模型中单位时间t，是一个应变量，受制于模型拟合时给定的条件。本例整个流行期79天，以初始时间t0为起点，相邻单位时间相隔约5天(79/17)，而且自t0起，每隔3个单位时间(约15天)所对应的日期与表1中各代中位潜伏期基本吻合。虽然按单位时间计算的理论例数难于与按代统计的实际例数进行拟合，但经拟合，实际资料同模型拟合良好。
, 百拇医药
K-M模型涉及一组微分方程，看似复杂，实则计算起来并不难，尤其能用图示表达各要素之间的数量关系，更适于教学。此外，本模型引入
项，β为传染性接触率，γ为恢复率，即感染者转变为下一代免疫者的概率，这是动力学模型两个敏感参数，使得模型具有更大的普适性。当然，数学模型优点只表现在数学方面是不够的，重要的是对方程中各项的设计和各种状态的转移作出合理的解释。应当说K-M模型结构中未考虑隐性感染者，这固然使模型显得较为简洁与明快，但反过来也使其应用范围受到限制。本文仅对国内记录较完整的一起传染病在特定人群中流行过程作模拟，K-M模型是否能成功应用于其他场合，尚待进一步考验。参考文献
[1]沈福民. 理论流行病学. 见：耿贯一(主编). 流行病学. 第1卷.第2版. 北京：人民卫生出版社, 1995: 288～290
, http://www.100md.com
[2]苏德隆(主编). 流行病学. 北京: 人民卫生出版社, 1964: 90～94
[3]连志浩(主编). 流行病学. 北京: 人民卫生出版社, 1994: 127～128
[4]曾 光(主编).现代流行病学方法与应用. 北京:北京医科大学、中国协和医科大学联合出版社, 1994: 203～208
[5]曾 光. 一种Reed-Frost确定型模型的修改型及其应用. 中华流行病学杂志, 1986; 7: 366
(收稿：1998-11-05 修回：1999-01-28), http://www.100md.com