纵向观测计数数据的对数线性模型
作者：熊林平 曹秀堂 徐勇勇 郭祖超
单位：熊林平 第二军医大学卫生统计学教研室(200433); 曹秀堂 徐勇勇 郭祖超 第四军医大学卫生统计学教研室(710032)
关键词：纵向数据；计数数据；广义估计方程
中国卫生统计990202 【提 要】 目的 纵向观测数据是按时间顺序对个体的某一变量进行多次观测获得的资料。本文利用广义线性模型对纵向计数数据进行了分析，充分考虑重复观测间的相关性。方法 采用Zeger和Liang提出的广义估计方程，在拟合对数广义线性模型的同时，引入偏离参数，讨论三种协方差矩阵的结构。结果 同时获得回归参数、相关参数、偏离参数的估计，完成了较为实用的运行程序，并进行了实例讨论。结论 医学研究和临床试验中经常接触到纵向观测数据，对这类数据需采用特殊的方法进行分析处理。
Generalized log-linear Models for Longitudinal Count Data
, 百拇医药
Xiong Linping,et al.,Department of Health Statistics,Second Military Medical University(200433),Shanghai
【Abstract】 Objective The defining characteristic of logitudinal data is that individuals are measured repeatedly through time.This thesis used generalized linear models to analyze longitudinal count data.The correlation between repeated measures was considered.Methods Generalized estimating equations(GEE)proposed by Zeger and Liang were used.While fitted generalized loglinear models,we introduced dispersed parameters for three covariance structures.Results Regression,correlation and dispersed parameters were estimated simultaneously.A program was finished and an example was illustrated.Conclusion Longitudinal data often occur in medical researches and clinical trials.It is necessary to use some special methods to cope with this kind of data.
, http://www.100md.com
【Key words】 Longitudinal data Count data Generalized estimating equations
纵向观测数据是按时间顺序对个体进行重复观测得到的资料。对于纵向观测资料，若采用通常意义下的方差分析等横向分析方法，由于忽略了重复观测间的相关性，将导致信息损失、参数估计不准确甚至错误的结论。
纵向研究充分考虑了数据间的相互依赖性，具有提高功效以及对模型的选择具有稳健性等优点。其研究的焦点集中在如何解决重复观测间的相关性问题上〔1，2〕。Zeger和Liang在1986年提出的广义估计方程，较好地解决了似然函数中多余参数的估计问题〔3，4〕。
本文讨论纵向观测计数数据的对数广义线性模型，利用广义估计方程解决模型的回归参数和相关参数的估计问题。
, http://www.100md.com
模型及参数估计
我们以一个实例引入纵向观测计数数据：
某医院考察纤维素对痉挛儿童便秘的缓解作用，选患儿30名，先观察6周作为基线数据，记录每周的灌肠次数；从第7周开始，每天服用含纤维素15g的食物，服用两周半，然后停用一周半，第11周到第17周每天服用含纤维素19g的食物，逐周记录灌肠次数。研究目的是：(1)纤维素对便秘有无缓解作用；(2)不同用量的纤维素对便秘的缓解作用是否相同。观测结果见表1。数据部分9表示缺失。
表1 30名痉挛儿童的便秘治疗结果 编号
基 线
纤维素(15g/日)
停
纤维素(19g/日)
, 百拇医药
1
2
3
4
5
6
7
8
9
10
11
12
13
14
, 百拇医药
15
16
17
1
0
1
2
1
1
1
0
0
0
2
, http://www.100md.com
1
2
2
1
1
0
1
2
1
9
1
2
1
1
, 百拇医药
1
1
0
0
0
1
1
0
1
0
1
3
9
2
, 百拇医药
2
1
2
2
0
1
1
1
0
1
0
1
0
1
, 百拇医药
2………………………………………………
29
2
9
9
9
9
1
0
1
0
2
1
, 百拇医药 1
2
2
1
1
1
30
2
9
0
9
9
1
1
, 百拇医药
1
1
1
1
2
2
2
2
1
0
*：数据部分9表示缺失数据
一般地，设有m个个体，个体i的观测序列为yi=(yi1,…，yini)′，相应的观测时间为ti=(ti1,…，tini)′。对应于yij的协变量向量为xij=(xij1，…，xijp)′，以Yij表示对应于yij的随机变量，记μij=E(Yij),μi=(μi1，…，μini)′。为方便起见，下面的叙述中，去掉ni的下标i。
, 百拇医药
计数数据表示一定时间内某事件的发生数，通常用Poisson分布描述：
Pr{Y=y}=μye-μ/y!，y=0,1,…
有Var(Y)=E(Y)。对于计数数据的纵向观测序列yi=(yi1,…，yin′)，模型假定为
log(μij)=x′ijβ
其中β为回归参数向量。实际数据往往方差与均值偏离过大，对于这种非Poisson分布描述的超离散数据，引入偏离参数τ，假定
Var(Yij)=φijE(Yij),φij>0
, http://www.100md.com
φij依赖于偏离参数向量τ，φij=φ(τ)。以上的模型讨论限于等距观测，若为不等距观测，对数线性模型为
log(μij)=log(sij)+x′ijβ
(1)
其中sij为观测时间间隔，若记ti0=0，即首次观测记为零时刻，则有关系式
sij=tij-tij-1 j=1,…，n
以α表示相关参数向量，记γ=(α′、τ′)′，则回归参数β的广义估计方程为〔3〕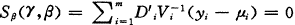
, http://www.100md.com
(2)
其中 Di=
μi/β=(dik)n×p
Ai=diag{φi1μi1，…，φinμin}
Ri(α)为依赖于相关参数向量α的近似相关阵。由(1)式知
djk=sijxijkexp(x′ijβ) j=1,…，n；k=1,…，p
, http://www.100md.com
可见，估计方程(2)包含三种参数：回归参数β、相关参数α、偏离参数τ。γ满足下列方程〔5〕：
(3)
其中，Wi=(yi1yi2,…，yin-1yin,
,…，
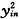)′为
n(n+1)/2维向量，而
ηi=E(Wi)
, 百拇医药
Hi=ηi/γ
在均值向量ηi中，须确定E(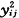
)(j=1,…，n)以及E(yijyik)(1≤jij)=E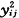-(Eyij)2知
(4)
, 百拇医药
根据相关系数的定义式
得
E(yijyik)=μijμik+δijk(φijμijφikμik)1/2
(5)
估计未知参数γ、β的迭代公式为
βs+1=βs+(ΣiD′iV-1iDi)-1ΣiD′iV-1i(yi-μi)
, 百拇医药
(6)
γs+1=γs+(ΣiH′iHi)-1ΣiH′i(Wi-ηi)
(7)
其中Σ为求和符号。将δijk看作近似相关阵Ri(α)的(j,k)元，考虑Ri(α)的三种假定结构，获得(7)式中的ηi和Hi。下面的讨论中总假定偏离参数φij=φ，则(4)、(5)式变为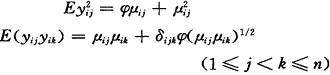
相关阵结构
, http://www.100md.com
1.独立结构(IND)
此时R(α)=I为单位矩阵，表明每个个体的各次重复观测间相互独立，相关系数δijk=0(j≠k),ηi和Hi分别为
2.一阶依赖结构(DE-1)
此时R(α)为三对角阵，δij,j+1=α (j=1,…，n-1)
即ηi中的元素E(yijyik)为
, http://www.100md.com
Hi为n*×2阶矩阵，n*=n(n+1)/2，Hi的结构为
其中H3=(0,…，0)′为n维零向量，H4=(μi1，…，μin)′为n维向量。
以ηi1表示ηi的前n(n-1)项构成的向量，即
ηi1=(μi1μi1+αφ(μi1μi2)1/2，μi1μi3，…，μin-1μin+αφ(μin-1μin)1/2)′
, http://www.100md.com
则
H1=ηi1/α，H2=ηi1/φ
因此，H1中的元素h1r(r=1,…，n(n-1)/2)与其在ηi1中的对应项E(yijyik)有关，即有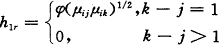
, 百拇医药
同样，H2的元素h2r(r=1,…，n(n-1)/2)有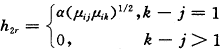
2.可交换结构(EXC)
此时δijk=α(j≠k)，即假定同一个体的各次观测间相关性相同。类似于一阶依赖结构，可以导出迭代公式(6)、(7)中所需的ηi与Hi。
协方差阵的稳健估计
假设已由对数线性模型获得参数估计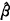
、
、
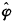，记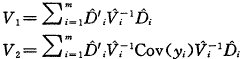
, http://www.100md.com
其中Cov(yi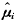)=(yi-
)(yi-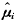)′。则β的协方差阵的稳健估计为〔4〕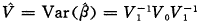
我们已将上述方法编制成计算机运行程序，下面用表1实例说明纵向计数数据的分析方法。
实例分析
图1表示逐周平均灌肠次数，由图1可见，作为基线的前六周，每周平均灌肠次数均大于一次，第7周服用纤维素后，小于一次，第9周为第一清洗期，灌肠次数依然小于1，可见纤维素有残留效应，第10周为第二清洗期，灌肠次数基本恢复到基线水平，第11周以后再次服用纤维素，平均次数又小于1。
, http://www.100md.com
观测时间(周)
图1 痉挛患儿每周平均灌肠次数
由以上分析，拟合对数线性模型，将观测时间分为五个阶段，阶段Ⅰ为前六周，此间不作治疗；阶段Ⅱ为第7、8两周，每天服用纤维素15g；阶段Ⅲ为第9周，此为第一清洗期，前半周每天服用纤维素15g，后半周停服；阶段Ⅳ为第10周，为第二清洗期，此间完全停服纤维素；阶段Ⅴ为最后7周，每天服用纤维素19g。引入如下协变量：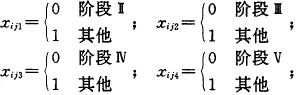
拟合模型Ⅰ
log(μij)=β0+xij1β1+xij2β2+xij3β3+xij4β4
, http://www.100md.com
i=1,…，30；j=1,…，17
于是可按观察阶段分别写出模型
(1)第Ⅰ阶段(基线)
log(μij)=β0+β1+β2+β3+β4，j=1,…，6
(2)第Ⅱ阶段(纤维素15g/日)
log(μij)=β0+β2+β3+β4，j=7，8
(3)第Ⅲ阶段(清洗期1)
, http://www.100md.com log(μij)=β0+β1+β3+β4，j=9
(4)第Ⅳ阶段(清洗期2)
log(μij)=β0+β1+β2+β4，j=10
(5)第Ⅴ阶段(纤维素19g/日)
log(μij)=β0+β1+β2+β3，j=11，…，17
因此，exp(β1)为阶段Ⅰ与阶段Ⅱ的灌肠次数均值比，exp(β1)>1表示纤维素对便秘有缓解作用；exp(β2)为阶段Ⅰ与阶段Ⅲ的均值比等等。
, http://www.100md.com
讨 论
我们对述三种相关阵结构进行了模型拟合，参数估计结果见表2。由表2可见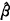，1≈0.47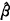，4≈0.455，说明每天服用含纤维素15g或纤维素19g的食物对便秘均有缓解作用。每天服用纤维素15g可减少灌肠次数60%{=exp(0.47)-1}，每天服用纤维素19g可减少灌肠次数58%{=exp(0.455)-1}。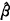2≈0.40，说明维生素有残留效应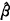；3≈0.075，exp(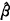3)≈1，且此项无显著性意义，可见阶段Ⅱ对阶段Ⅴ的影响已经消除。另外若采用独立结构(IND)，即不考虑重复观测间的相关性，估计值与标准误的比值较之其他两种相关阵结构大多偏大，容易得出显著性的结论，即易犯Ⅰ型错误。三种相关阵结构估计的偏参数φ均靠近0.63，与样本值φ=(0.815)2/0.959=0.69接近，可见估计偏离参数有实际意义。
, 百拇医药
表2 对数线性模型Ⅰ拟合结果 参数
相关结构
估计值
标准误
估计值/
标准误
β0
IND
-1.2022
0.3310
3.6318
DE-1
, http://www.100md.com
-1.1573
0.3497
3.3096
EXC
-1.1707
0.3389
3.4546
β1
IND
0.4760
0.1355
3.5119
, 百拇医药
DE-1
0.4682
0.1421
3.2938
EXC
0.4680
0.1388
3.3729
β2
IND
0.4141
0.1342
, 百拇医药 3.0860
DE-1
0.3714
0.1519
2.4444
EXC
0.4061
0.1379
2.9441
β3
IND
0.0777
0.1125
, 百拇医药
0.6905
DE-1
0.0861
0.1177
0.7341
EXC
0.0697
0.1126
0.6185
β4
IND
0.4662
, 百拇医药 0.0805
5.7928
DE-1
0.4539
0.0784
5.7902
EXC
0.4507
0.0785
5.7383
α
IND
DE-1
, http://www.100md.com
0.246
EXC
0.205
φ
IND
0.619
DE-1
0.634
EXC
0.627
为考察纤维素用量的不同是否对便秘的缓解作用也不同，引入如下协变量：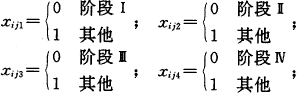
, 百拇医药
拟合模型Ⅱ
log(μij)=β0+xij1β1+xij2β2+xij3β3+xij4β4
i=1,…，30；j=1,…，17
纤维素的用量效应由exp(β2)决定，若exp(β2)=1，则表明纤维素的多少对便秘的缓解作用无明显差异。结果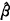2≈0.014，exp(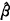2)≈1且此效应无显著性意义，说明每天服用纤维素15g与服用纤维素19g对便秘的缓解作用相同。
, http://www.100md.com
参考文献
1.Zeger SL and Liang KY.An overview of methods for the analysis of longitudinal data.Statistics in Medicine,1992，11:1825～1839.
2.Hendricks SA,Wassell JT,Collins JW et al.Power determination for geographically clustered data using generalized estimating equations.Statistics in Medicine.1996，15:1951～1960
3.Liang KY and Zeger SL.Longitudinal data analysis using generalized linear models.Biometrika,1986，73(1):13～22.
4.Zeger SL and Liang KY.Longitudinal data analysis for discrete and continuous outcomes.Biometrics,1986，42(1):121～130.
5.Diggle PJ,Liang KY and Zeger SL.Analysis of longitudinal data.Oxford Statistical Science Series 13,Oxford University Press.1994., http://www.100md.com
单位：熊林平 第二军医大学卫生统计学教研室(200433); 曹秀堂 徐勇勇 郭祖超 第四军医大学卫生统计学教研室(710032)
关键词：纵向数据；计数数据；广义估计方程
中国卫生统计990202 【提 要】 目的 纵向观测数据是按时间顺序对个体的某一变量进行多次观测获得的资料。本文利用广义线性模型对纵向计数数据进行了分析，充分考虑重复观测间的相关性。方法 采用Zeger和Liang提出的广义估计方程，在拟合对数广义线性模型的同时，引入偏离参数，讨论三种协方差矩阵的结构。结果 同时获得回归参数、相关参数、偏离参数的估计，完成了较为实用的运行程序，并进行了实例讨论。结论 医学研究和临床试验中经常接触到纵向观测数据，对这类数据需采用特殊的方法进行分析处理。
Generalized log-linear Models for Longitudinal Count Data
, 百拇医药
Xiong Linping,et al.,Department of Health Statistics,Second Military Medical University(200433),Shanghai
【Abstract】 Objective The defining characteristic of logitudinal data is that individuals are measured repeatedly through time.This thesis used generalized linear models to analyze longitudinal count data.The correlation between repeated measures was considered.Methods Generalized estimating equations(GEE)proposed by Zeger and Liang were used.While fitted generalized loglinear models,we introduced dispersed parameters for three covariance structures.Results Regression,correlation and dispersed parameters were estimated simultaneously.A program was finished and an example was illustrated.Conclusion Longitudinal data often occur in medical researches and clinical trials.It is necessary to use some special methods to cope with this kind of data.
, http://www.100md.com
【Key words】 Longitudinal data Count data Generalized estimating equations
纵向观测数据是按时间顺序对个体进行重复观测得到的资料。对于纵向观测资料，若采用通常意义下的方差分析等横向分析方法，由于忽略了重复观测间的相关性，将导致信息损失、参数估计不准确甚至错误的结论。
纵向研究充分考虑了数据间的相互依赖性，具有提高功效以及对模型的选择具有稳健性等优点。其研究的焦点集中在如何解决重复观测间的相关性问题上〔1，2〕。Zeger和Liang在1986年提出的广义估计方程，较好地解决了似然函数中多余参数的估计问题〔3，4〕。
本文讨论纵向观测计数数据的对数广义线性模型，利用广义估计方程解决模型的回归参数和相关参数的估计问题。
, http://www.100md.com
模型及参数估计
我们以一个实例引入纵向观测计数数据：
某医院考察纤维素对痉挛儿童便秘的缓解作用，选患儿30名，先观察6周作为基线数据，记录每周的灌肠次数；从第7周开始，每天服用含纤维素15g的食物，服用两周半，然后停用一周半，第11周到第17周每天服用含纤维素19g的食物，逐周记录灌肠次数。研究目的是：(1)纤维素对便秘有无缓解作用；(2)不同用量的纤维素对便秘的缓解作用是否相同。观测结果见表1。数据部分9表示缺失。
表1 30名痉挛儿童的便秘治疗结果 编号
基 线
纤维素(15g/日)
停
纤维素(19g/日)
, 百拇医药
1
2
3
4
5
6
7
8
9
10
11
12
13
14
, 百拇医药
15
16
17
1
0
1
2
1
1
1
0
0
0
2
, http://www.100md.com
1
2
2
1
1
0
1
2
1
9
1
2
1
1
, 百拇医药
1
1
0
0
0
1
1
0
1
0
1
3
9
2
, 百拇医药
2
1
2
2
0
1
1
1
0
1
0
1
0
1
, 百拇医药
2………………………………………………
29
2
9
9
9
9
1
0
1
0
2
1
, 百拇医药 1
2
2
1
1
1
30
2
9
0
9
9
1
1
, 百拇医药
1
1
1
1
2
2
2
2
1
0
*：数据部分9表示缺失数据
一般地，设有m个个体，个体i的观测序列为yi=(yi1,…，yini)′，相应的观测时间为ti=(ti1,…，tini)′。对应于yij的协变量向量为xij=(xij1，…，xijp)′，以Yij表示对应于yij的随机变量，记μij=E(Yij),μi=(μi1，…，μini)′。为方便起见，下面的叙述中，去掉ni的下标i。
, 百拇医药
计数数据表示一定时间内某事件的发生数，通常用Poisson分布描述：
Pr{Y=y}=μye-μ/y!，y=0,1,…
有Var(Y)=E(Y)。对于计数数据的纵向观测序列yi=(yi1,…，yin′)，模型假定为
log(μij)=x′ijβ
其中β为回归参数向量。实际数据往往方差与均值偏离过大，对于这种非Poisson分布描述的超离散数据，引入偏离参数τ，假定
Var(Yij)=φijE(Yij),φij>0
, http://www.100md.com
φij依赖于偏离参数向量τ，φij=φ(τ)。以上的模型讨论限于等距观测，若为不等距观测，对数线性模型为
log(μij)=log(sij)+x′ijβ
(1)
其中sij为观测时间间隔，若记ti0=0，即首次观测记为零时刻，则有关系式
sij=tij-tij-1 j=1,…，n
以α表示相关参数向量，记γ=(α′、τ′)′，则回归参数β的广义估计方程为〔3〕
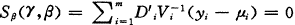
, http://www.100md.com
(2)
其中 Di=
μi/β=(dik)n×pAi=diag{φi1μi1，…，φinμin}
Ri(α)为依赖于相关参数向量α的近似相关阵。由(1)式知
djk=sijxijkexp(x′ijβ) j=1,…，n；k=1,…，p
, http://www.100md.com
可见，估计方程(2)包含三种参数：回归参数β、相关参数α、偏离参数τ。γ满足下列方程〔5〕：
(3)
其中，Wi=(yi1yi2,…，yin-1yin,
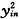,…，)′为n(n+1)/2维向量，而
ηi=E(Wi)
, 百拇医药
Hi=
ηi/γ在均值向量ηi中，须确定E(
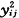)(j=1,…，n)以及E(yijyik)(1≤j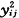-(Eyij)2知(4)
, 百拇医药
根据相关系数的定义式
得
E(yijyik)=μijμik+δijk(φijμijφikμik)1/2
(5)
估计未知参数γ、β的迭代公式为
βs+1=βs+(ΣiD′iV-1iDi)-1ΣiD′iV-1i(yi-μi)
, 百拇医药
(6)
γs+1=γs+(ΣiH′iHi)-1ΣiH′i(Wi-ηi)
(7)
其中Σ为求和符号。将δijk看作近似相关阵Ri(α)的(j,k)元，考虑Ri(α)的三种假定结构，获得(7)式中的ηi和Hi。下面的讨论中总假定偏离参数φij=φ，则(4)、(5)式变为
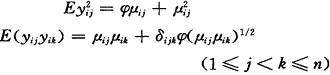
相关阵结构
, http://www.100md.com
1.独立结构(IND)
此时R(α)=I为单位矩阵，表明每个个体的各次重复观测间相互独立，相关系数δijk=0(j≠k),ηi和Hi分别为
2.一阶依赖结构(DE-1)
此时R(α)为三对角阵，δij,j+1=α (j=1,…，n-1)
即ηi中的元素E(yijyik)为
, http://www.100md.com
Hi为n*×2阶矩阵，n*=n(n+1)/2，Hi的结构为
其中H3=(0,…，0)′为n维零向量，H4=(μi1，…，μin)′为n维向量。
以ηi1表示ηi的前n(n-1)项构成的向量，即
ηi1=(μi1μi1+αφ(μi1μi2)1/2，μi1μi3，…，μin-1μin+αφ(μin-1μin)1/2)′
, http://www.100md.com
则
H1=
ηi1/α，H2=ηi1/φ因此，H1中的元素h1r(r=1,…，n(n-1)/2)与其在ηi1中的对应项E(yijyik)有关，即有
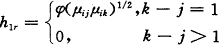
, 百拇医药
同样，H2的元素h2r(r=1,…，n(n-1)/2)有
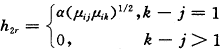
2.可交换结构(EXC)
此时δijk=α(j≠k)，即假定同一个体的各次观测间相关性相同。类似于一阶依赖结构，可以导出迭代公式(6)、(7)中所需的ηi与Hi。
协方差阵的稳健估计
假设已由对数线性模型获得参数估计
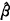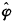、、，记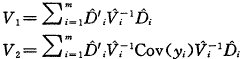, http://www.100md.com
其中Cov(yi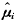)=(yi-
)(yi-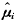)′。则β的协方差阵的稳健估计为〔4〕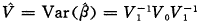我们已将上述方法编制成计算机运行程序，下面用表1实例说明纵向计数数据的分析方法。
实例分析
图1表示逐周平均灌肠次数，由图1可见，作为基线的前六周，每周平均灌肠次数均大于一次，第7周服用纤维素后，小于一次，第9周为第一清洗期，灌肠次数依然小于1，可见纤维素有残留效应，第10周为第二清洗期，灌肠次数基本恢复到基线水平，第11周以后再次服用纤维素，平均次数又小于1。
, http://www.100md.com
观测时间(周)
图1 痉挛患儿每周平均灌肠次数
由以上分析，拟合对数线性模型，将观测时间分为五个阶段，阶段Ⅰ为前六周，此间不作治疗；阶段Ⅱ为第7、8两周，每天服用纤维素15g；阶段Ⅲ为第9周，此为第一清洗期，前半周每天服用纤维素15g，后半周停服；阶段Ⅳ为第10周，为第二清洗期，此间完全停服纤维素；阶段Ⅴ为最后7周，每天服用纤维素19g。引入如下协变量：
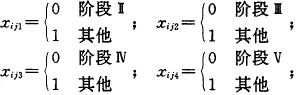
拟合模型Ⅰ
log(μij)=β0+xij1β1+xij2β2+xij3β3+xij4β4
, http://www.100md.com
i=1,…，30；j=1,…，17
于是可按观察阶段分别写出模型
(1)第Ⅰ阶段(基线)
log(μij)=β0+β1+β2+β3+β4，j=1,…，6
(2)第Ⅱ阶段(纤维素15g/日)
log(μij)=β0+β2+β3+β4，j=7，8
(3)第Ⅲ阶段(清洗期1)
, http://www.100md.com log(μij)=β0+β1+β3+β4，j=9
(4)第Ⅳ阶段(清洗期2)
log(μij)=β0+β1+β2+β4，j=10
(5)第Ⅴ阶段(纤维素19g/日)
log(μij)=β0+β1+β2+β3，j=11，…，17
因此，exp(β1)为阶段Ⅰ与阶段Ⅱ的灌肠次数均值比，exp(β1)>1表示纤维素对便秘有缓解作用；exp(β2)为阶段Ⅰ与阶段Ⅲ的均值比等等。
, http://www.100md.com
讨 论
我们对述三种相关阵结构进行了模型拟合，参数估计结果见表2。由表2可见，
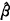1≈0.47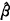，4≈0.455，说明每天服用含纤维素15g或纤维素19g的食物对便秘均有缓解作用。每天服用纤维素15g可减少灌肠次数60%{=exp(0.47)-1}，每天服用纤维素19g可减少灌肠次数58%{=exp(0.455)-1}。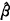2≈0.40，说明维生素有残留效应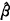；3≈0.075，exp(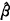3)≈1，且此项无显著性意义，可见阶段Ⅱ对阶段Ⅴ的影响已经消除。另外若采用独立结构(IND)，即不考虑重复观测间的相关性，估计值与标准误的比值较之其他两种相关阵结构大多偏大，容易得出显著性的结论，即易犯Ⅰ型错误。三种相关阵结构估计的偏参数φ均靠近0.63，与样本值φ=(0.815)2/0.959=0.69接近，可见估计偏离参数有实际意义。, 百拇医药
表2 对数线性模型Ⅰ拟合结果 参数
相关结构
估计值
标准误
估计值/
标准误
β0
IND
-1.2022
0.3310
3.6318
DE-1
, http://www.100md.com
-1.1573
0.3497
3.3096
EXC
-1.1707
0.3389
3.4546
β1
IND
0.4760
0.1355
3.5119
, 百拇医药
DE-1
0.4682
0.1421
3.2938
EXC
0.4680
0.1388
3.3729
β2
IND
0.4141
0.1342
, 百拇医药 3.0860
DE-1
0.3714
0.1519
2.4444
EXC
0.4061
0.1379
2.9441
β3
IND
0.0777
0.1125
, 百拇医药
0.6905
DE-1
0.0861
0.1177
0.7341
EXC
0.0697
0.1126
0.6185
β4
IND
0.4662
, 百拇医药 0.0805
5.7928
DE-1
0.4539
0.0784
5.7902
EXC
0.4507
0.0785
5.7383
α
IND
DE-1
, http://www.100md.com
0.246
EXC
0.205
φ
IND
0.619
DE-1
0.634
EXC
0.627
为考察纤维素用量的不同是否对便秘的缓解作用也不同，引入如下协变量：
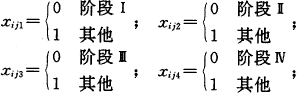
, 百拇医药
拟合模型Ⅱ
log(μij)=β0+xij1β1+xij2β2+xij3β3+xij4β4
i=1,…，30；j=1,…，17
纤维素的用量效应由exp(β2)决定，若exp(β2)=1，则表明纤维素的多少对便秘的缓解作用无明显差异。结果
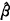2≈0.014，exp(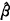2)≈1且此效应无显著性意义，说明每天服用纤维素15g与服用纤维素19g对便秘的缓解作用相同。, http://www.100md.com
参考文献
1.Zeger SL and Liang KY.An overview of methods for the analysis of longitudinal data.Statistics in Medicine,1992，11:1825～1839.
2.Hendricks SA,Wassell JT,Collins JW et al.Power determination for geographically clustered data using generalized estimating equations.Statistics in Medicine.1996，15:1951～1960
3.Liang KY and Zeger SL.Longitudinal data analysis using generalized linear models.Biometrika,1986，73(1):13～22.
4.Zeger SL and Liang KY.Longitudinal data analysis for discrete and continuous outcomes.Biometrics,1986，42(1):121～130.
5.Diggle PJ,Liang KY and Zeger SL.Analysis of longitudinal data.Oxford Statistical Science Series 13,Oxford University Press.1994., http://www.100md.com