一种用于电阻抗成像的拟Newton算法—基于修正Bk的开关算法
作者:李文波 王博亮 孙桂菊 向飞 刘希顺
单位:李文波 孙桂菊 向飞(北京航天医学工程研究所 北京 100094);王博亮 刘希顺(国防科技大学电子技术学院 长沙 410073)
关键词:电阻抗成像;重建算法;拟Newton法;逆问题
北京生物医学工程000104 摘 要 本文提出了一种新的电阻抗成像(EIT)图像重建算法—基于修正Bk的拟Newton类算法,并通过数值试验验证了该算法的有效性。新算法基于目标函数梯度向量的快速算法,利用基于修正Bk的拟Newton法来求解EIT逆问题。与著名的Newton-Raphson算法相比,该算法的突出优点是计算量小,数值稳定性好,具有整体收敛性。
A Quasi-Newton Algorithm for Electrical Impedance Tomography
, http://www.100md.com
—a Switch Algorithm Based on Modified Bk
Li Wenbo
(Institute of Space Medical Engineering, Beijing 100094)
Wang Boliang
(Department of Electronic Technology, National University of Defense Technology, ChangSha 410073)
Sun Guiju
(Institute of Space Medical Engineering, Beijing 100094)
, http://www.100md.com
Xiang Fei
(Institute of Space Medical Engineering, Beijing 100094)
Liu Xishun
(Department of Electronic Technology, National University of Defense Technology, ChangSha 410073)
Abstract
In this paper we propose a new image reconstruction algorithm for electrical impedance tomography-Quasi-Newton algorithm, based on modified Bk. Numerical tests were made to verify the effectiveness of this algorithm. Based on the fast algorithm for calculating gradient vectors of object function, this new algorithm makes use of Quasi-Newton algorithm based on modified Bk to solve the inverse problem of EIT. Comparing this new algorithm with the famous Newton-Raphson method, the outstandng advantages of this new algorithm are that the workload of computation can be reduced, and numerical stability and integral convergence can be obtained.
, http://www.100md.com
Key words:Electrical impedance tomography; Reconstruction algorithm; Quasi-Newten algorithm; Invere problem
0 引 言
电阻抗成像(electrical impedance tomography, EIT)作为一种功能性医学成像技术的研究始于70年代末。由于它具有设备简单、成本低廉、对人体无害、不要求特殊的工作环境等优点,使其成为近年来生物医学工程界的研究热点之一。
EIT的数学模型由下述椭圆形方程边值问题描述[1]: (1)
(1)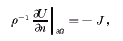 , (2)
, (2) (3)
(3)
, http://www.100md.com
其中Ω为物体所在的空间区域, 为其边界,U为求解区域的电势分布,V、J分别为边界电压和边界电流密度分布,ρ为待求电阻率分布。与一般的偏微分方程的定解问题不同,这里的系数ρ和电势分布U都是未知的,而且我们要求解的正是物体的电阻率分布ρ,因此这是一个二阶椭圆形方程未知系数辨识的逆问题(inverse problem)。
为其边界,U为求解区域的电势分布,V、J分别为边界电压和边界电流密度分布,ρ为待求电阻率分布。与一般的偏微分方程的定解问题不同,这里的系数ρ和电势分布U都是未知的,而且我们要求解的正是物体的电阻率分布ρ,因此这是一个二阶椭圆形方程未知系数辨识的逆问题(inverse problem)。
对于区域Ω,在边界电流密度J给定的条件下,记电阻率分布到边界电压分布之间的映射为F(ρ)=V,其中ρ、V分别属于一适当的函数空间(离散化后为两个有限维空间)。EIT算法包括两部分:求解正问题和逆问题。在ρ设定的情况下,求F(ρ)的过程称为EIT的正问题。考虑到EIT问题的特点,一般用有限元方法求解EIT正问题,此时求解区域离散成许多小单元(三角形或四边形),ρ以某种插值函数的形式表示。记F的离散形式为f,则f为两个有限维空间之间的映射:Rm→Rn,f(ρ)=v。在ρ未知的情况下,利用已知的边界条件求ρ的问题称为EIT的逆问题。EIT的逆问题通常要用最优化方法求解。
, 百拇医药
实践中,为了获取尽可能多的关于电阻率分布ρ的信息,一般采用多次施加电流的方法,进行多次边界电压测量。设共有ρ次线性独立的电流模式注入,相应的正问题的解及边界电压测量值分别记为fi(ρ)和vi(i=1,2,…,p),则EIT逆问题离散化后成为下面的非线性最小二乘问题:
minφ(ρ), (4)
其中 (5)
(5)
对于EIT逆问题,现在已有许多重建算法,其中理论上较完善、重建效果较好的算法是Newton-Raphson算法及其改进形式[2],本质上是求解上述非线性最小二乘问题(4)、(5)的Gauss-Newton法和LM法。但是,Newton-Raphson算法的缺点也是明显的,主要是:计算量大,而且随空间分辨率的提高,计算量迅速增长;数值稳定性不够好;只有局部收敛性。针对Newton-Raphson算法的这些缺点,文献[3]导出了一种目标函数梯度向量的快速算法,在此基础上提出了一种基于修正Hk的拟Newton法(组合变尺度法)用于求解EIT逆问题。与Newton-Raphson算法相比,拟Newton法的性能明显要好:拟Newton法的计算量随空间分辨率提高而增长的速度比Newton-Raphson算法要慢得多;而且该算法具有整体收敛性,因此迭代初值的选取比较方便;拟Newton法的数值稳定性也明显好于Newton-Raphson算法,因此拟Newton法有更强的抗扰动能力。由于上述优点,使拟Newton类算法在求解EIT逆问题方面成为一类很有竞争力的算法。
, http://www.100md.com
1 用基于修正Bk的拟Newton法求解EIT逆问题
1.1 数值稳定性分析
我们知道,拟Newton法是求解一般无约束最优化问题的一种重要方法。它的基本思想是:利用初始给定的对称正定矩阵Bk和Hk作为对目标函数的Hesse矩阵或Hesse矩阵的逆矩阵的估计,选定迭代初值,利用目标函数的梯度向量和Bk或Hk矩阵计算出下降方向,进行迭代。在迭代过程中不断修正Bk和Hk,使算法在不用Hesse矩阵的情况下具有Newton法的某些优良性质,因此它是一类非常有效的算法。
常用的修正Bk的公式有两个,分别称为关于Bk的DFP公式和BFGS公式;常用的修正Hk的公式也有两个,分别称为关于Hk的DFP公式和BFGS公式[4]。实际计算时,DFP公式和BFGS公式可单独使用,也可以结合起来构成所谓的开关算法(又称组合变尺度法)。一般认为,组合变尺度法的数值稳定性较普通的拟Newton算法更好。
, http://www.100md.com
文献[3]导出了求解EIT逆问题的基于修正Hk的拟Newton法,同样我们也可以用基于修正Bk的拟Newton法来求解EIT问题。而且,文献[5]中指出,基于修正Bk的拟Newton法比基于修正Hk的拟Newton法有更高的数值稳定性。为了以后讨论方便,我们先给出修正Bk的DFP公式, (6)
(6)
和BFGS公式, (7)
(7)
以及修正Hk的DFP公式, (8)
(8)
和BFGS公式, (9)
(9)
, 百拇医药
其中sk=ρk+1-ρk,yk=gk+1-gk;ρk为第k次迭代时的电阻率分布向量,gk为第k次迭代时的梯度向量。比较上面四个公式可以看出,修正Bk需要计算ykyTk/sTkyk;修正Hk需要计算sssTk/sTkyk。假定Sk、yk均有计算误差ε,则计算ykyTk/sTkyk和计算sksTk/STkyk的误差分别为O([yk22/sTkyk].ε)和O([‖Sk‖22/sTkyk].ε)。文献[5]指出,存在常数M,使得yk22k22。而反过来有可能sk/yk→∞。以上说明,修正Bk带来的计算误差比修正Hk带来的计算误差要小得多,因此,基于修正Bk的拟Newton法的数值稳定性要比基于修正Hk的拟Newton法有很大提高。
, 百拇医药
1.2 修正矩阵的Cholesky分解
下面我们讨论基于修正Bk的拟Newton算法的构造。为便于讨论,我们先对修正Bk的DFP公式(6)作一变换。式(6)可改写为[4]: (10)
(10)
其中 ηk=gTkpk,tk=(μ2kδk-1)gk+gk+1。
ηk=gTkpk,tk=(μ2kδk-1)gk+gk+1。
在基于修正Bk的拟Newton法中,为求搜索方向Pk,应求解方程组
, 百拇医药
Bkpk=-gk (11)
由于直接求解(11)式的计算量比基于修正Hk的拟Newton法要大,所以一般不直接求解(11)式,而采用Bk的Cholesky分解形式Bk=LkDkLTk,从解方程组
LkDkLTkpk=-gk (12)
确定pk°为了进一步提高这种做法的效率,最好能根据Bk的修正公式(6)、(7)导出相应的Lk和Dk的迭代公式,以便直接由Lk和Dk求和Lk+1和Dk+1,而不必每次迭代都进行一次Cholesky分解。
, http://www.100md.com
下面讨论修正矩阵的Cholesky分解方法:
记Bk=LkDkLTk,Bk+1=Lk+1Dk+1LTk+1,若已知Lk、Dk,从原则上说,由式(6)或(7)可以求出修正矩阵Bk+1的Cholesky分解因子Lk+1和Dk+1,这一步骤称为修正矩阵的Cholesky分解。通过观察,可以发现,不论是BFGS公式(7),还是DFP公式(10),Bk+1都是由Bk加上两个修正项得到的,这两个修正项具有相同的形式σZZT(其中是σ纯量,Z是n维向量)。因此修正矩阵的Cholesky分解可以分成两步进行,每一步都是对加上一个形如σZZT的修正项的矩阵进行分解。这就是说,我们只需考虑下列问题:设已知B=LDLT和σ、Z,求B.=B+σZZT的Cholesky因子L.和D.,使得
, http://www.100md.com
B.=B+σZZT=LDLT+σZZT=L*D*L*T (13)
文献[11]中给出了两种计算方法:一种是利用Householder变换的算法;另一种称为基于“对比”的算法。这里介绍基于“对比”的算法。
设 是方程组
是方程组 的解,则
的解,则
对 进行分解
进行分解
, 百拇医药
这里 是单位下三角阵,
是单位下三角阵, 是对角阵,则
是对角阵,则
令
最后得到B.=L.D.L.T。很明显,这里L.是单位下三角阵,D.是对角阵,它们就是B.的Cholesky分解因子。
, 百拇医药
下面给出分解 的计算公式。
的计算公式。
设
记 为由
为由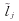 的后面n-s+1个元素组成的n-s+1维向量(s,j=1,…,n),
的后面n-s+1个元素组成的n-s+1维向量(s,j=1,…,n), 的后面n-i+1个元素组成的n-i+1维向量(i=1,…,n),可以证明(详细证明过程见文献[4])
的后面n-i+1个元素组成的n-i+1维向量(i=1,…,n),可以证明(详细证明过程见文献[4])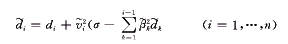 (14)
(14) (15)
(15) (16)
(16)
, http://www.100md.com
于是我们得到
这样,我们就可以采用相应的BFGS公式(7)或DFP公式(10),通过两次调用上述修正矩阵的Cholesky分解算法,得到修正矩阵的Cholesky分解因子Lk+1和Dk+1。
1.3 基于修正Bk的拟Newton法的计算步骤
有了上面的准备工作,我们就可以构造出基于修正Bk的拟Newton类算法。下面给出利用基于修正Bk的开关算法求解EIT反问题的具体计算步骤[4]:
(1)取定ρ0,N,ε,W;其中,W为一正定矩阵,例如,可以取为单位阵I;N为控制迭代次数的整数;ε为控制迭代精度的量;
, 百拇医药
(2)令ρk=ρ0,gk=φ′(ρk),Bk=W,k=1;
(3)判断gk<ε?若成立,停止计算,ρ=ρk。否则转下步
(4)对Bk进行Cholesky分解,得Lk,Dk;
(5)判断k≥N?若成立,停止计算,ρ=ρk。否则转下步;
(6)依次解方程组 确定搜索方向pk;
确定搜索方向pk;
(7)作一维搜索求λk,使得:
, 百拇医药
φ(ρk+λkpk)=min{φ(pk+λpk)λ≥0,令Sk=λkpk,ρk+1=ρk+λkpk,计算gk+1=φ.(ρk+1),yk=gk+1-gk;
(8)判断gk+1<ε若成立,停止计算,ρ=ρk+1。否则转下步;
(9)令dk=-λkgk,a=sTkdk,b=sTkyk;
, 百拇医药
(10)判断b≤a?若成立,转(11);否则转(12);
(11)采用BFGS公式(7),调用两次修正矩阵的Cholesky分解算法,得Lk+1和Dk+1,转(13);
(12)采用DFP公式(10),调用两次修正矩阵的Cholesky分解算法,得Lk+1和Dk+1,转(13);
(13)令gk=gk+1,ρk=ρk+1;
(14)k=k+1,转(5)。
2 数值试验
为验证上述基于修正Bk的开关算法的有效性并分析其性能,我们对Newton-Raphson算法(LM法)和基于修正Bk的开关算法进行了数值试验。
, http://www.100md.com
图1 计算模型的有限元网格
试验所用的有限元模型如图1所示,采用28电极进行数据采集,注入正弦型电流模型,进行27次独立测量。通过在边界电压数据中加上1%的扰动(用(-1,1)内均匀分布的随机数进行扰动)后进行重建,来说明各算法的数值稳定性。各电阻率分量的迭代初值均取为1。LM算法的迭代次数为20次,基于修正Bk的开关算法的迭代次数为100次。背景电阻率均为10,电阻率的单位为Ω.cm。
下面是对两种真实电阻率分布模型的重建图像。每幅图像旁边的灰度卡都标出了各图像中的最大、最小电阻率值所对应的灰度值,其余电阻率值对应的灰度值在最大、最小值之间均匀分布。
图2 目标在中心时的重建图像
, http://www.100md.com
其中(b)、(c)分别为不加扰动时的重建图像;(d)、(e)分别为加1%扰动时的重建图像。
比较以上各重建图像,可以看出:在无扰动的情况下,基于修正Bk的开关算法与Newton-Raphson类算法的重建效果处于同一水平;而在边界电压加扰动的情况下,基于修正Bk的开关算法的重建效果明显好于Newton-Raphson类算法。这说明基于修正Bk的开关算法的数值稳定性比Newton-Raphson类算法更好,由于实际测量的边界电压都不可避免干扰,因此,拟Newton类算法更加实用。
图3 目标在边界时的重建图像
其中(b)、(c)分别为不加扰动时的重建图像;(d)、(e)分别为加1%扰动时的重建图像。
, 百拇医药
同时,我们的数值试验表明,基于修正Bk的开关算法迭代100次所用的时间与Newton-Raphson类算法迭代20次所用的时间相同。虽然基于修正Bk的开关算法所需的迭代次数要多一点,但其总的计算量仍要比Newton-Raphson类算法少。而且,该算法的迭代初值的选取比较容易。
3 结 论
本文通过对拟Newton类算法的分析与研究,提出并实现了一种新的EIT重建算法—基于修正Bk的拟Newton类算法。与Newton-Raphson类算法(LM算法)相比,新算法的数值稳定性有了明显的改进;同时,新算法的计算量也有所减少,特别是其计算量随空间分辨率提高而增长的速度比Newton-Raphson算法要慢得多;而且该算法具有整体收敛性,因此迭代初值的选取比较方便。
本研究得到了北京航空航天大学孙进平博士和程吉宽教授的帮助和指导,在此表示衷心感谢!
, 百拇医药
作者简介:李文波(1969—)男,助理研究员。
4 参考文献
[1] Webster J G. Electrical impedance tomography. Bristol England, Adam Hilger, 1990,97-137
[2] Yorkey T J, et al. Compairing reconstruction algorithms for electrical impedance tomography. IEEE Trans Biomed Eng, 1987, BME-34(11):843-852
[3] 杜岩,程吉宽,柳重堪.用组合变尺度法求解电阻抗成像问题.中国生物医学工程学报,1997,16(2):167-173
[4] 邓乃扬著.无约束最优化计算方法.科学出版社,1982:128-205
[5] 袁亚湘著.非线性规则数值方法.上海科学技术出版社,1993:114-116
(1999-01-21收稿,1999-04-05修回), 百拇医药
单位:李文波 孙桂菊 向飞(北京航天医学工程研究所 北京 100094);王博亮 刘希顺(国防科技大学电子技术学院 长沙 410073)
关键词:电阻抗成像;重建算法;拟Newton法;逆问题
北京生物医学工程000104 摘 要 本文提出了一种新的电阻抗成像(EIT)图像重建算法—基于修正Bk的拟Newton类算法,并通过数值试验验证了该算法的有效性。新算法基于目标函数梯度向量的快速算法,利用基于修正Bk的拟Newton法来求解EIT逆问题。与著名的Newton-Raphson算法相比,该算法的突出优点是计算量小,数值稳定性好,具有整体收敛性。
A Quasi-Newton Algorithm for Electrical Impedance Tomography
, http://www.100md.com
—a Switch Algorithm Based on Modified Bk
Li Wenbo
(Institute of Space Medical Engineering, Beijing 100094)
Wang Boliang
(Department of Electronic Technology, National University of Defense Technology, ChangSha 410073)
Sun Guiju
(Institute of Space Medical Engineering, Beijing 100094)
, http://www.100md.com
Xiang Fei
(Institute of Space Medical Engineering, Beijing 100094)
Liu Xishun
(Department of Electronic Technology, National University of Defense Technology, ChangSha 410073)
Abstract
In this paper we propose a new image reconstruction algorithm for electrical impedance tomography-Quasi-Newton algorithm, based on modified Bk. Numerical tests were made to verify the effectiveness of this algorithm. Based on the fast algorithm for calculating gradient vectors of object function, this new algorithm makes use of Quasi-Newton algorithm based on modified Bk to solve the inverse problem of EIT. Comparing this new algorithm with the famous Newton-Raphson method, the outstandng advantages of this new algorithm are that the workload of computation can be reduced, and numerical stability and integral convergence can be obtained.
, http://www.100md.com
Key words:Electrical impedance tomography; Reconstruction algorithm; Quasi-Newten algorithm; Invere problem
0 引 言
电阻抗成像(electrical impedance tomography, EIT)作为一种功能性医学成像技术的研究始于70年代末。由于它具有设备简单、成本低廉、对人体无害、不要求特殊的工作环境等优点,使其成为近年来生物医学工程界的研究热点之一。
EIT的数学模型由下述椭圆形方程边值问题描述[1]:
 (1)
(1)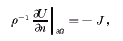 , (2)
, (2) (3)
(3), http://www.100md.com
其中Ω为物体所在的空间区域,
 为其边界,U为求解区域的电势分布,V、J分别为边界电压和边界电流密度分布,ρ为待求电阻率分布。与一般的偏微分方程的定解问题不同,这里的系数ρ和电势分布U都是未知的,而且我们要求解的正是物体的电阻率分布ρ,因此这是一个二阶椭圆形方程未知系数辨识的逆问题(inverse problem)。
为其边界,U为求解区域的电势分布,V、J分别为边界电压和边界电流密度分布,ρ为待求电阻率分布。与一般的偏微分方程的定解问题不同,这里的系数ρ和电势分布U都是未知的,而且我们要求解的正是物体的电阻率分布ρ,因此这是一个二阶椭圆形方程未知系数辨识的逆问题(inverse problem)。对于区域Ω,在边界电流密度J给定的条件下,记电阻率分布到边界电压分布之间的映射为F(ρ)=V,其中ρ、V分别属于一适当的函数空间(离散化后为两个有限维空间)。EIT算法包括两部分:求解正问题和逆问题。在ρ设定的情况下,求F(ρ)的过程称为EIT的正问题。考虑到EIT问题的特点,一般用有限元方法求解EIT正问题,此时求解区域离散成许多小单元(三角形或四边形),ρ以某种插值函数的形式表示。记F的离散形式为f,则f为两个有限维空间之间的映射:Rm→Rn,f(ρ)=v。在ρ未知的情况下,利用已知的边界条件求ρ的问题称为EIT的逆问题。EIT的逆问题通常要用最优化方法求解。
, 百拇医药
实践中,为了获取尽可能多的关于电阻率分布ρ的信息,一般采用多次施加电流的方法,进行多次边界电压测量。设共有ρ次线性独立的电流模式注入,相应的正问题的解及边界电压测量值分别记为fi(ρ)和vi(i=1,2,…,p),则EIT逆问题离散化后成为下面的非线性最小二乘问题:
minφ(ρ), (4)
其中
 (5)
(5)对于EIT逆问题,现在已有许多重建算法,其中理论上较完善、重建效果较好的算法是Newton-Raphson算法及其改进形式[2],本质上是求解上述非线性最小二乘问题(4)、(5)的Gauss-Newton法和LM法。但是,Newton-Raphson算法的缺点也是明显的,主要是:计算量大,而且随空间分辨率的提高,计算量迅速增长;数值稳定性不够好;只有局部收敛性。针对Newton-Raphson算法的这些缺点,文献[3]导出了一种目标函数梯度向量的快速算法,在此基础上提出了一种基于修正Hk的拟Newton法(组合变尺度法)用于求解EIT逆问题。与Newton-Raphson算法相比,拟Newton法的性能明显要好:拟Newton法的计算量随空间分辨率提高而增长的速度比Newton-Raphson算法要慢得多;而且该算法具有整体收敛性,因此迭代初值的选取比较方便;拟Newton法的数值稳定性也明显好于Newton-Raphson算法,因此拟Newton法有更强的抗扰动能力。由于上述优点,使拟Newton类算法在求解EIT逆问题方面成为一类很有竞争力的算法。
, http://www.100md.com
1 用基于修正Bk的拟Newton法求解EIT逆问题
1.1 数值稳定性分析
我们知道,拟Newton法是求解一般无约束最优化问题的一种重要方法。它的基本思想是:利用初始给定的对称正定矩阵Bk和Hk作为对目标函数的Hesse矩阵或Hesse矩阵的逆矩阵的估计,选定迭代初值,利用目标函数的梯度向量和Bk或Hk矩阵计算出下降方向,进行迭代。在迭代过程中不断修正Bk和Hk,使算法在不用Hesse矩阵的情况下具有Newton法的某些优良性质,因此它是一类非常有效的算法。
常用的修正Bk的公式有两个,分别称为关于Bk的DFP公式和BFGS公式;常用的修正Hk的公式也有两个,分别称为关于Hk的DFP公式和BFGS公式[4]。实际计算时,DFP公式和BFGS公式可单独使用,也可以结合起来构成所谓的开关算法(又称组合变尺度法)。一般认为,组合变尺度法的数值稳定性较普通的拟Newton算法更好。
, http://www.100md.com
文献[3]导出了求解EIT逆问题的基于修正Hk的拟Newton法,同样我们也可以用基于修正Bk的拟Newton法来求解EIT问题。而且,文献[5]中指出,基于修正Bk的拟Newton法比基于修正Hk的拟Newton法有更高的数值稳定性。为了以后讨论方便,我们先给出修正Bk的DFP公式,
 (6)
(6)和BFGS公式,
 (7)
(7)以及修正Hk的DFP公式,
 (8)
(8)和BFGS公式,
 (9)
(9), 百拇医药
其中sk=ρk+1-ρk,yk=gk+1-gk;ρk为第k次迭代时的电阻率分布向量,gk为第k次迭代时的梯度向量。比较上面四个公式可以看出,修正Bk需要计算ykyTk/sTkyk;修正Hk需要计算sssTk/sTkyk。假定Sk、yk均有计算误差ε,则计算ykyTk/sTkyk和计算sksTk/STkyk的误差分别为O([yk22/sTkyk].ε)和O([‖Sk‖22/sTkyk].ε)。文献[5]指出,存在常数M,使得yk22
, 百拇医药
1.2 修正矩阵的Cholesky分解
下面我们讨论基于修正Bk的拟Newton算法的构造。为便于讨论,我们先对修正Bk的DFP公式(6)作一变换。式(6)可改写为[4]:
 (10)
(10)其中
 ηk=gTkpk,tk=(μ2kδk-1)gk+gk+1。
ηk=gTkpk,tk=(μ2kδk-1)gk+gk+1。在基于修正Bk的拟Newton法中,为求搜索方向Pk,应求解方程组
, 百拇医药
Bkpk=-gk (11)
由于直接求解(11)式的计算量比基于修正Hk的拟Newton法要大,所以一般不直接求解(11)式,而采用Bk的Cholesky分解形式Bk=LkDkLTk,从解方程组
LkDkLTkpk=-gk (12)
确定pk°为了进一步提高这种做法的效率,最好能根据Bk的修正公式(6)、(7)导出相应的Lk和Dk的迭代公式,以便直接由Lk和Dk求和Lk+1和Dk+1,而不必每次迭代都进行一次Cholesky分解。
, http://www.100md.com
下面讨论修正矩阵的Cholesky分解方法:
记Bk=LkDkLTk,Bk+1=Lk+1Dk+1LTk+1,若已知Lk、Dk,从原则上说,由式(6)或(7)可以求出修正矩阵Bk+1的Cholesky分解因子Lk+1和Dk+1,这一步骤称为修正矩阵的Cholesky分解。通过观察,可以发现,不论是BFGS公式(7),还是DFP公式(10),Bk+1都是由Bk加上两个修正项得到的,这两个修正项具有相同的形式σZZT(其中是σ纯量,Z是n维向量)。因此修正矩阵的Cholesky分解可以分成两步进行,每一步都是对加上一个形如σZZT的修正项的矩阵进行分解。这就是说,我们只需考虑下列问题:设已知B=LDLT和σ、Z,求B.=B+σZZT的Cholesky因子L.和D.,使得
, http://www.100md.com
B.=B+σZZT=LDLT+σZZT=L*D*L*T (13)
文献[11]中给出了两种计算方法:一种是利用Householder变换的算法;另一种称为基于“对比”的算法。这里介绍基于“对比”的算法。
设
 是方程组
是方程组 的解,则
的解,则
对
 进行分解
进行分解
, 百拇医药
这里
 是单位下三角阵,
是单位下三角阵, 是对角阵,则
是对角阵,则
令

最后得到B.=L.D.L.T。很明显,这里L.是单位下三角阵,D.是对角阵,它们就是B.的Cholesky分解因子。
, 百拇医药
下面给出分解
 的计算公式。
的计算公式。设

记
 为由
为由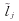 的后面n-s+1个元素组成的n-s+1维向量(s,j=1,…,n),
的后面n-s+1个元素组成的n-s+1维向量(s,j=1,…,n), 的后面n-i+1个元素组成的n-i+1维向量(i=1,…,n),可以证明(详细证明过程见文献[4])
的后面n-i+1个元素组成的n-i+1维向量(i=1,…,n),可以证明(详细证明过程见文献[4])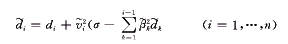 (14)
(14) (15)
(15) (16)
(16), http://www.100md.com
于是我们得到

这样,我们就可以采用相应的BFGS公式(7)或DFP公式(10),通过两次调用上述修正矩阵的Cholesky分解算法,得到修正矩阵的Cholesky分解因子Lk+1和Dk+1。
1.3 基于修正Bk的拟Newton法的计算步骤
有了上面的准备工作,我们就可以构造出基于修正Bk的拟Newton类算法。下面给出利用基于修正Bk的开关算法求解EIT反问题的具体计算步骤[4]:
(1)取定ρ0,N,ε,W;其中,W为一正定矩阵,例如,可以取为单位阵I;N为控制迭代次数的整数;ε为控制迭代精度的量;
, 百拇医药
(2)令ρk=ρ0,gk=φ′(ρk),Bk=W,k=1;
(3)判断gk<ε?若成立,停止计算,ρ=ρk。否则转下步
(4)对Bk进行Cholesky分解,得Lk,Dk;
(5)判断k≥N?若成立,停止计算,ρ=ρk。否则转下步;
(6)依次解方程组
 确定搜索方向pk;
确定搜索方向pk;(7)作一维搜索求λk,使得:
, 百拇医药
φ(ρk+λkpk)=min{φ(pk+λpk)λ≥0,令Sk=λkpk,ρk+1=ρk+λkpk,计算gk+1=φ.(ρk+1),yk=gk+1-gk;
(8)判断gk+1<ε若成立,停止计算,ρ=ρk+1。否则转下步;
(9)令dk=-λkgk,a=sTkdk,b=sTkyk;
, 百拇医药
(10)判断b≤a?若成立,转(11);否则转(12);
(11)采用BFGS公式(7),调用两次修正矩阵的Cholesky分解算法,得Lk+1和Dk+1,转(13);
(12)采用DFP公式(10),调用两次修正矩阵的Cholesky分解算法,得Lk+1和Dk+1,转(13);
(13)令gk=gk+1,ρk=ρk+1;
(14)k=k+1,转(5)。
2 数值试验
为验证上述基于修正Bk的开关算法的有效性并分析其性能,我们对Newton-Raphson算法(LM法)和基于修正Bk的开关算法进行了数值试验。

, http://www.100md.com
图1 计算模型的有限元网格
试验所用的有限元模型如图1所示,采用28电极进行数据采集,注入正弦型电流模型,进行27次独立测量。通过在边界电压数据中加上1%的扰动(用(-1,1)内均匀分布的随机数进行扰动)后进行重建,来说明各算法的数值稳定性。各电阻率分量的迭代初值均取为1。LM算法的迭代次数为20次,基于修正Bk的开关算法的迭代次数为100次。背景电阻率均为10,电阻率的单位为Ω.cm。
下面是对两种真实电阻率分布模型的重建图像。每幅图像旁边的灰度卡都标出了各图像中的最大、最小电阻率值所对应的灰度值,其余电阻率值对应的灰度值在最大、最小值之间均匀分布。

图2 目标在中心时的重建图像
, http://www.100md.com
其中(b)、(c)分别为不加扰动时的重建图像;(d)、(e)分别为加1%扰动时的重建图像。
比较以上各重建图像,可以看出:在无扰动的情况下,基于修正Bk的开关算法与Newton-Raphson类算法的重建效果处于同一水平;而在边界电压加扰动的情况下,基于修正Bk的开关算法的重建效果明显好于Newton-Raphson类算法。这说明基于修正Bk的开关算法的数值稳定性比Newton-Raphson类算法更好,由于实际测量的边界电压都不可避免干扰,因此,拟Newton类算法更加实用。

图3 目标在边界时的重建图像
其中(b)、(c)分别为不加扰动时的重建图像;(d)、(e)分别为加1%扰动时的重建图像。
, 百拇医药
同时,我们的数值试验表明,基于修正Bk的开关算法迭代100次所用的时间与Newton-Raphson类算法迭代20次所用的时间相同。虽然基于修正Bk的开关算法所需的迭代次数要多一点,但其总的计算量仍要比Newton-Raphson类算法少。而且,该算法的迭代初值的选取比较容易。
3 结 论
本文通过对拟Newton类算法的分析与研究,提出并实现了一种新的EIT重建算法—基于修正Bk的拟Newton类算法。与Newton-Raphson类算法(LM算法)相比,新算法的数值稳定性有了明显的改进;同时,新算法的计算量也有所减少,特别是其计算量随空间分辨率提高而增长的速度比Newton-Raphson算法要慢得多;而且该算法具有整体收敛性,因此迭代初值的选取比较方便。
本研究得到了北京航空航天大学孙进平博士和程吉宽教授的帮助和指导,在此表示衷心感谢!
, 百拇医药
作者简介:李文波(1969—)男,助理研究员。
4 参考文献
[1] Webster J G. Electrical impedance tomography. Bristol England, Adam Hilger, 1990,97-137
[2] Yorkey T J, et al. Compairing reconstruction algorithms for electrical impedance tomography. IEEE Trans Biomed Eng, 1987, BME-34(11):843-852
[3] 杜岩,程吉宽,柳重堪.用组合变尺度法求解电阻抗成像问题.中国生物医学工程学报,1997,16(2):167-173
[4] 邓乃扬著.无约束最优化计算方法.科学出版社,1982:128-205
[5] 袁亚湘著.非线性规则数值方法.上海科学技术出版社,1993:114-116
(1999-01-21收稿,1999-04-05修回), 百拇医药